. For fNIRS, Y is the time series of fNIRS measurements, X is the design matrix including all regressors, is the coefficients to be estimated for each regressor, and is the the error term which is assumed to be spherical Gaussian N(0,). The model is typically solved via generalized ordinary least squares: =XTX-1XTY
cov(β)=(X^T X)^(-1)
In order for this solution to be the best linear unbiased estimate of the coefficients, the Gauss-Markov assumptions have to be fulfilled, namely linearity, random sampling, non-collinearity, strict exogeneity and spherical errors.
Alternative definition:
Synonym:
References: https://doi.org/10.1007/978-1-59745-530-5_10
Related terms: Linear regression, Generalized Linear Mixed Model, regression
General linear model
Definition: Your General linear model is a linear regression model that allows for analyzing data ( Y ) according to a given set of regressors often also referred to as predictors in the context of experiment design, (X) by estimating fit coefficients (). The general equation of the GLM is: 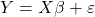. For fNIRS, Y is the time series of fNIRS measurements, X is the design matrix including all regressors, is the coefficients to be estimated for each regressor, and is the the error term which is assumed to be spherical Gaussian N(0,). The model is typically solved via generalized ordinary least squares: =XTX-1XTY
cov(β)=(X^T X)^(-1)
In order for this solution to be the best linear unbiased estimate of the coefficients, the Gauss-Markov assumptions have to be fulfilled, namely linearity, random sampling, non-collinearity, strict exogeneity and spherical errors.
Alternative definition:
Synonym:
References: https://doi.org/10.1007/978-1-59745-530-5_10
Related terms: Linear regression, Generalized Linear Mixed Model, regression
. For fNIRS, Y is the time series of fNIRS measurements, X is the design matrix including all regressors, is the coefficients to be estimated for each regressor, and is the the error term which is assumed to be spherical Gaussian N(0,). The model is typically solved via generalized ordinary least squares: =XTX-1XTY
cov(β)=(X^T X)^(-1)
In order for this solution to be the best linear unbiased estimate of the coefficients, the Gauss-Markov assumptions have to be fulfilled, namely linearity, random sampling, non-collinearity, strict exogeneity and spherical errors.
Alternative definition:
Synonym:
References: https://doi.org/10.1007/978-1-59745-530-5_10
Related terms: Linear regression, Generalized Linear Mixed Model, regression