Definition: The fast Fourier transform (FFT) is a family of algorithms that computes a sequence’s Fourier transform (FT) by decomposing a series of values into components with distinct frequencies. The distinctive characteristic of this family of algorithms is their computational efficiency; they reduce the number of computations for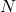
points from N
to
.
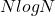Alternative definition: Fast Fourier Transforms (FFT) is a family of efficient algorithms that computes the Fourier Transform (FT) of a sequence of data points. The discrete FT transforms a time-domain signal into its frequency-domain representation, which can be used to analyze and manipulate the signal. (Note, the use of terms time and frequency here are not intended in their physical meaning. Fourier transform can be applied to mathematical sets with no physical semantics.)
Synonym:
References: https://doi.org/10.1109/MSPEC.1967.5217220
Related terms: Fourier transform, Discrete Fourier transform
