Definition: In signal processing, filter order refers to the number of poles (or zeros) in the transfer function of a filter. Poles and zeros are locations in the complex plane where the transfer function becomes infinite or zero, respectively. The order of a filter is equal to the number of poles or zeros, whichever is greater.The filter order is an important parameter because it determines the steepness of the filter’s cutoff slope and its overall performance. Generally speaking, higher-order filters have steeper cutoff slopes, which means they can more effectively attenuate unwanted frequencies while passing desired frequencies. However, higher-order filters also require more computational resources and can introduce more phase distortion, so there is often a trade-off between filter performance and complexity.
The filter order can be mathematically represented as the highest power of the variable in the transfer function of the filter.
For example, a first-order low-pass filter has a transfer function of the form:
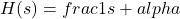where s is the complex frequency variable and
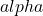is a constant. The filter order in this case is 1, since the highest power of s in the denominator is 1.
Similarly, a second-order high-pass filter has a transfer function of the form:
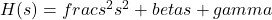where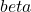
and
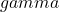are constants. The filter order in this case is 2, since the highest power of s in the denominator is 2.
In general, the filter order can be determined by counting the number of poles (or zeros) in the transfer function, or by finding the highest power of the variable in the transfer function.
Alternative definition: The order of the filter refers to the maximum delay in samples used in generating each output sample. The higher the order the steeper the slope between passband and stopband.
Synonym:
References: http://www.w3k.org/
ISBN 10: 0974560715
https://doi.org/10.1504/IJWMC.2018.089991
Related terms: Filter, FIR FIlter, IIR Filter, Preprocessing
