from a vector space X over the field of real or complex numbers into the real numbers that abides by the principle of superposition. Norms are often a measure of an object size and hence they are distance functions (from the origin) e.g. metrics. There exist a myriad of norms with Lebesgue’s Lp norms being perhaps the most familiar.The specific case of the L1 norm is a popular choice as a penalty term in regularization techniques to encourage sparse solutions. In fNIRS analysis, the L1 norm has found many uses; for instance in image reconstruction. It has also been used in sparsity regularization, where the goal is to identify the regions of the brain that are most active during a task. Sparsity regularization involves adding a penalty term to the objective function that is minimized when estimating the changes in hemoglobin concentration. The penalty term encourages the solution to have many zero or near-zero coefficients, which indicates that only a few regions of the brain are active during the task.
Alternative definition:
Synonym:
References: https://encyclopediaofmath.org/wiki/Norm
W. Rudin, “Functional analysis” , McGraw-Hill (1979)
https://doi.org/10.1007/978-3-662-09000-8
Related terms:
L1 norm
Definition: The L1 norm is the p=1 norm case of Lebesgue’s Lp spaces. Norms are positive mappings 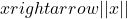from a vector space X over the field of real or complex numbers into the real numbers that abides by the principle of superposition. Norms are often a measure of an object size and hence they are distance functions (from the origin) e.g. metrics. There exist a myriad of norms with Lebesgue’s Lp norms being perhaps the most familiar.The specific case of the L1 norm is a popular choice as a penalty term in regularization techniques to encourage sparse solutions. In fNIRS analysis, the L1 norm has found many uses; for instance in image reconstruction. It has also been used in sparsity regularization, where the goal is to identify the regions of the brain that are most active during a task. Sparsity regularization involves adding a penalty term to the objective function that is minimized when estimating the changes in hemoglobin concentration. The penalty term encourages the solution to have many zero or near-zero coefficients, which indicates that only a few regions of the brain are active during the task.
Alternative definition:
Synonym:
References: https://encyclopediaofmath.org/wiki/Norm
W. Rudin, “Functional analysis” , McGraw-Hill (1979)
https://doi.org/10.1007/978-3-662-09000-8
Related terms:
from a vector space X over the field of real or complex numbers into the real numbers that abides by the principle of superposition. Norms are often a measure of an object size and hence they are distance functions (from the origin) e.g. metrics. There exist a myriad of norms with Lebesgue’s Lp norms being perhaps the most familiar.The specific case of the L1 norm is a popular choice as a penalty term in regularization techniques to encourage sparse solutions. In fNIRS analysis, the L1 norm has found many uses; for instance in image reconstruction. It has also been used in sparsity regularization, where the goal is to identify the regions of the brain that are most active during a task. Sparsity regularization involves adding a penalty term to the objective function that is minimized when estimating the changes in hemoglobin concentration. The penalty term encourages the solution to have many zero or near-zero coefficients, which indicates that only a few regions of the brain are active during the task.
Alternative definition:
Synonym:
References: https://encyclopediaofmath.org/wiki/Norm
W. Rudin, “Functional analysis” , McGraw-Hill (1979)
https://doi.org/10.1007/978-3-662-09000-8
Related terms: