from a vector space X over the field of real or complex numbers into the real numbers that abides by the principle of superposition. Norms are often a measure of an object size and hence they are distance functions (from the origin) e.g. metrics. There exist a myriad of norms with Lebesgue’s Lp norms being perhaps the most familiar.
Alternative definition:
Synonym:
References: https://encyclopediaofmath.org/wiki/Norm
W. Rudin, “Functional analysis” , McGraw-Hill (1979)
https://doi.org/10.1007/978-3-662-09000-8
Related terms: L1 Norm
Norm
Definition: Norms are positive mappings 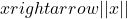from a vector space X over the field of real or complex numbers into the real numbers that abides by the principle of superposition. Norms are often a measure of an object size and hence they are distance functions (from the origin) e.g. metrics. There exist a myriad of norms with Lebesgue’s Lp norms being perhaps the most familiar.
Alternative definition:
Synonym:
References: https://encyclopediaofmath.org/wiki/Norm
W. Rudin, “Functional analysis” , McGraw-Hill (1979)
https://doi.org/10.1007/978-3-662-09000-8
Related terms: L1 Norm
from a vector space X over the field of real or complex numbers into the real numbers that abides by the principle of superposition. Norms are often a measure of an object size and hence they are distance functions (from the origin) e.g. metrics. There exist a myriad of norms with Lebesgue’s Lp norms being perhaps the most familiar.
Alternative definition:
Synonym:
References: https://encyclopediaofmath.org/wiki/Norm
W. Rudin, “Functional analysis” , McGraw-Hill (1979)
https://doi.org/10.1007/978-3-662-09000-8
Related terms: L1 Norm